What is the "rule" or shortcut we use when raising an exponent to another exponent?
The exponent rules explicate how to solve various equations that — as you might expect — have exponents in them. Only there are several different kinds of exponent equations and exponential expressions, which can seem daunting... at first.
Mastering these basic exponent rules along with bones rules of logarithms (also known as "log rules") volition make your study of algebra very productive and enjoyable. Go along in mind that during this process, the lodge of operations will however utilize.
Like most math tactics, there are educational activity strategies you can utilize to make exponent rules easy to follow.
To assistance you teach these concepts we have a gratis exponent rules worksheet for y'all to download and apply in your class!
What are exponents?
Exponents, also known as powers, are values that prove how many times to multiply a base number by itself. For example, 43 is telling you to multiply four by itself 3 times.
43= 4 × 4 × 4 = 64
The number being raised by a power is known as the base, while the superscript number above it is the exponent or power.
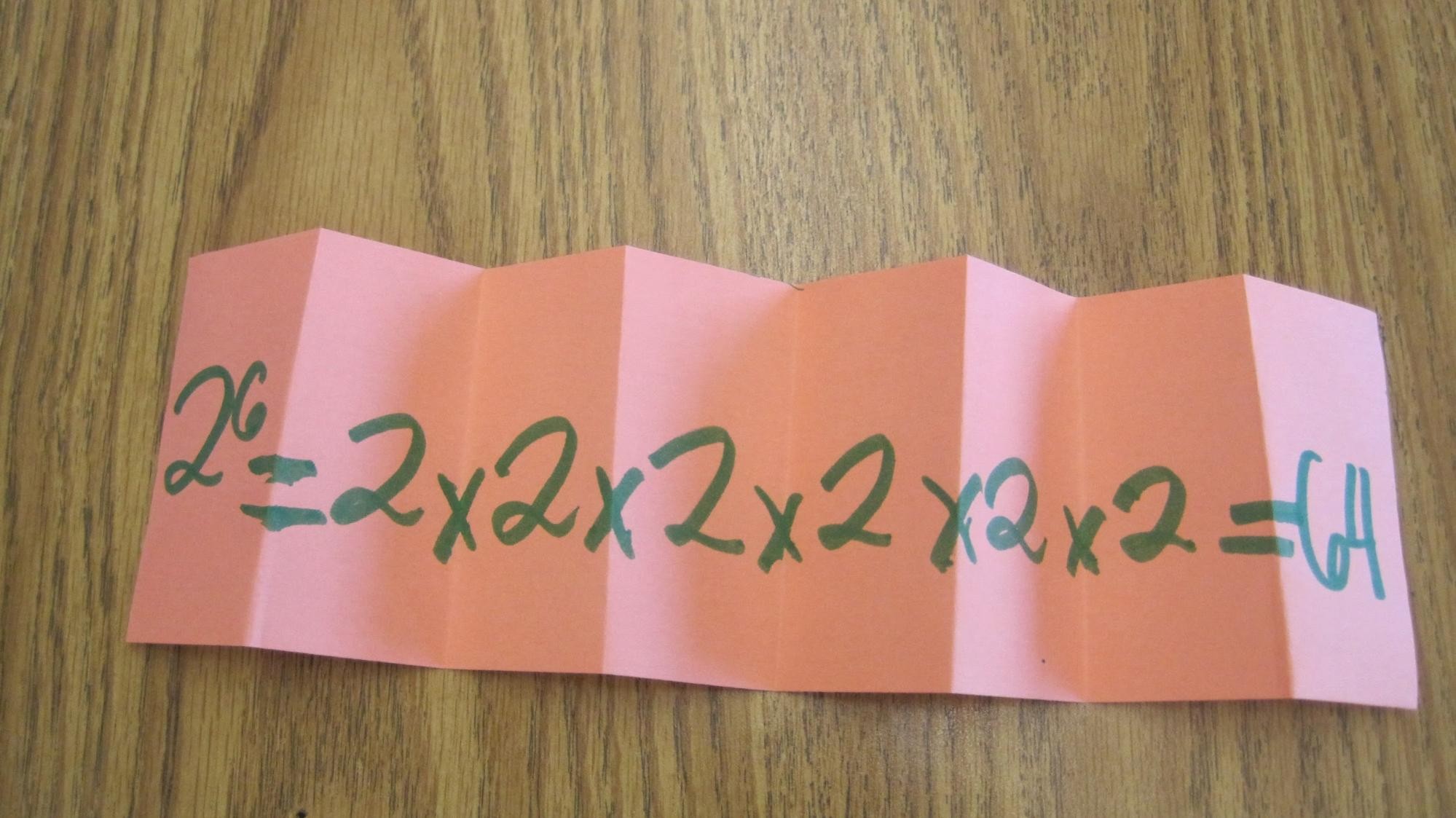
The equation to a higher place is said every bit "four to the power of three". The power of two can likewise exist said as "squared" and the power of 3 can be said every bit "cubed". These terms are ofttimes used when finding the area or volume of diverse shapes.
Writing a number in exponential form refers to simplifying it to a base with a power. For example, turning v × five × 5 into exponential form looks similar 53 .
Exponents are a way to simplify equations to make them easier to read. This becomes particularly important when you lot're dealing with variables such every bit 'π' and 'π¦' — as π7× π¦5= ? is easier to read than (π)(π)(π)(π)(π)(π)(π)(π¦)(π¦)(π¦)(π¦)(π¦) = ?
Rules of exponents in everyday life
Not only volition understanding exponent properties help y'all to solve various algebraic bug, exponents are besides used in a practical style in everyday life when calculating square anxiety, square meters, and even cubic centimeters.
Exponent rules also simplify calculating extremely large or extremely tiny quantities. These are also used in the globe of computers and technology when describing megabytes, gigabytes, and terabytes.
What are the different rules of exponents?
There are seven exponent rules, or laws of exponents, that your students need to learn. Each rule shows how to solve unlike types of math equations and how to add together, subtract, multiply and split exponents.
Make sure you become over each exponent rule thoroughly in class, as each one plays an of import role in solving exponent based equations.
1. Product of powers rule
When multiplying two bases of the aforementioned value, keep the bases the same and and so add the exponents together to become the solution.
four2× 45 = ?
Since the base values are both four, keep them the same and then add the exponents (2 + v) together.
42 × 45= 47
Then multiply four by itself seven times to get the answer.
4seven = four × 4 × iv × 4 × iv × 4 × 4 = sixteen,384
Let's expand the above equation to meet how this dominion works:
In an equation like this, adding the exponents together is a shortcut to go the reply.
Here's a more complicated question to endeavour:
(4πii)(2π3) = ?
Multiply the coefficients together (four and 2), as they are not the same base of operations. So keep the 'π' the same and add the exponents.
(4π2)(2πthree) = viiiπfive
ii. Caliber of powers rule
Multiplication and sectionalization are opposites of each other -- much the same, the quotient dominion acts as the opposite of the product rule.
When dividing two bases of the aforementioned value, keep the base of operations the same, and then subtract the exponent values.
55 ÷ 5three = ?
Both bases in this equation are five, which means they stay the aforementioned. And so, take the exponents and subtract the divisor from the dividend.
5five÷ 5iii = v2
Finally, simplify the equation if needed:
v2= 5 × 5 = 25
Once once again, expanding the equation shows usa that this shortcut gives the correct respond:
Accept a look at this more complicated instance:
5π4 / 10πii = ?
The similar variables in the denominator cancel out those in the numerator. You tin can show your students this by crossing out an equal number of π's from the top and bottom of the fraction.
5π4 / tenπ2 = 5π/10
Then simplify where possible, as you would with any fraction. Five can go into x, five times turning the fraction into ½ with the remaining π variables.
5πiv/xπtwo= iπ2/2 = π2/2
3. Ability of a power rule
This rule shows how to solve equations where a power is being raised by another ability.
(πthree)3 = ?
In equations similar the one above, multiply the exponents together and keep the base the same.
(π3)3 = π9
Take a look at the expanded equation to run into how this works:
four. Power of a product rule
When whatever base is existence multiplied by an exponent, distribute the exponent to each part of the base of operations.
(ππ¦)iii = ?
In this equation, the ability of iii needs to be distributed to both the π and the π¦ variables.
(ππ¦)3 = π3π¦3
This rule applies if there are exponents attached to the base besides.
(π2π¦two)iii = π6π¦6
Expanded, the equation would wait like this:
Both of the variables are squared in this equation and are existence raised to the power of three. That means three is multiplied to the exponents in both variables turning them into variables that are raised to the power of vi.
5. Ability of a quotient rule
A caliber simply means that you're dividing two quantities. In this rule, you're raising a caliber past a power. Like the power of a product rule, the exponent needs to be distributed to all values within the brackets information technology's attached to.
(π/π¦)4 = ?
Hither, heighten both variables within the brackets by the power of four.
Take a look at this more complicated equation:
(4π3/5π¦four)2 = ?
Don't forget to distribute the exponent you're multiplying by to both the coefficient and the variable. Then simplify where possible.
(ivπthree/vπ¦4)2= fourtwoπ6/52π¦8 = xviπ6/25π¦8
6. Nix power dominion
Any base of operations raised to the power of null is equal to i.
The easiest way to explicate this dominion is by using the quotient of powers dominion.
fouriii/iv3 = ?
Following the quotient of powers rule, subtract the exponents from each other, which cancels them out, merely leaving the base. Whatever number divided past itself is ane.
ivthree/43= four/iv = 1
No matter how long the equation, anything raised to the power of zilch becomes one.
(eighttwoπfourπ¦6)0 = ?
Typically, the outside exponent would have to be multiplied throughout each number and variable in the brackets. Nevertheless, since this equation is being raised to the power of zilch, these steps can be skipped and the answer only becomes 1.
(viii2π4π¦half-dozen)0 = 1
The equation fully expanded would look like this:
(8iiπ4π¦half dozen)0 = 80π0π¦0 = (1)(i)(1) = 1
7. Negative exponent rule
When in that location is a number being raised past a negative exponent, flip it into a reciprocal to turn the exponent into a positive. Don't use the negative exponent to turn the base into a negative.
We've talked near reciprocals before in our article, "How to carve up fractions in iii piece of cake steps". Essentially, reciprocals are what you multiply a number by to become the value of i. For case, to turn two into 1, multiply it by ½.
Now, look at this exponent case:
π-2 = ?
To make a number into a reciprocal:
- Plow the number into a fraction (put it over one)
- Flip the numerator into the denominator and vice versa
- When a negative number switches places in a fraction it becomes a positive number
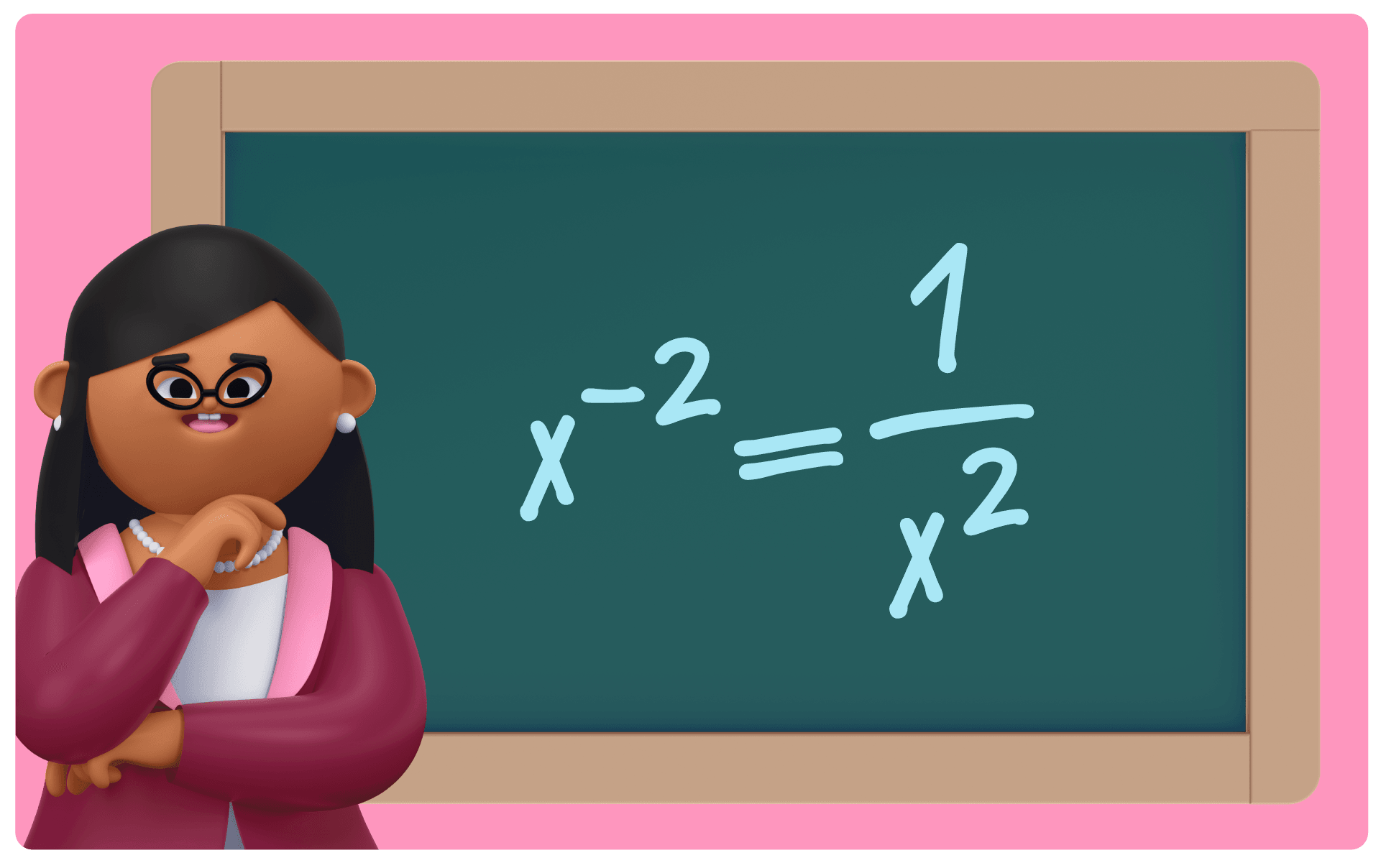
The goal of equations with negative exponents is to brand them positive.
Now, have a look at this more complicated equation:
fourπ-iiiπ¦2/20ππ§-3 = ?
In this equation, there are 2 exponents with negative powers. Simplify what you can, and then flip the negative exponents into their reciprocal form. In the solution, π-3 moves to the denominator, while π§-three moves to the numerator.
Since there is already an π value in the denominator, π3 adds to that value.
4π-3π¦2/20πz-3 = π¦2π§3/fiveπ4
With these seven rules in your students' back pockets, they'll exist able to accept on most exponent questions they come across!
Exponent rules chart
How Prodigy can assistance yous teach exponent rules
Prodigy is a curriculum-aligned math game yous tin use to assign questions, rail progress, and identify problem spots in your students' learning. And you lot can create teacher and educatee accounts for free!
With so many different exponent rules to follow and several students to rails, it tin exist hard to see who needs assistance with what. Prodigy makes it easy to track progress, and create a unique gaming experience for each student based on their needs.
Statistics are tracked live, as students play the game, and feedback is available instantly. Most of the fourth dimension your students won't fifty-fifty realize that they're taking part in math lessons. It's all role of their personalized gaming experience!
From the teacher dashboard, you can create lesson plans, see live statistics, input custom assignments, and gear up your students for upcoming tests. Hither's how y'all tin can employ Prodigy to:
- Prepare students for standardized tests
- Reinforce in-class concepts (like exponent rules)
- Differentiate math practice in the math classroom and at home
Complimentary exponent rules worksheet
Math worksheets are handy tools that can show how students are understanding central concepts. You tin can encounter how students are coming up with answers, where they're struggling, and if any concepts demand to be covered in more detail.
We've put together an exponent rules worksheet, with the assist of our squad of teachers, to help you with exponent lessons.
Click here to download our exponent rules worksheet, complete with an answer cardinal!
Conclusion: exponent rules practise
Exponents are used to show how many times a base of operations value is multiplied by itself. This simplifies equations to an easier to read format. (πππππππππ)(π¦π¦π¦π¦π¦π¦)(π§π§π§π§π§) = πnineπ¦6π§5
To epitomize, there are seven basic rules that explain how to solve most math equations that involve exponents. The exponent rules are:
- Product of powers rule — Add powers together when multiplying like bases
- Caliber of powers rule — Subtract powers when dividing like bases
- Power of powers rule — Multiply powers together when raising a power by another exponent
- Power of a product rule — Distribute power to each base of operations when raising several variables by a power
- Power of caliber rule — Distribute power to all values in a quotient
- Zero power rule — Any base raised to the power of zero becomes ane
- Negative exponent dominion — To change a negative exponent to a positive one, flip it into a reciprocal
Exponents accept a tendency of appearing throughout our lives, and then it'south important that students understand how they work moving forward. In that location are a lot of rules to recall but, one time your students understand them, solving exponents will likely become easier!
Prodigy Math Game is an adaptive, game-based learning platform. Success in Prodigy requires students to correctly answer curriculum-aligned questions adjusted to their learning needs, and gives teachers more ways to make math class fun! Sign up for your gratuitous instructor account today to get started.
Source: https://www.prodigygame.com/main-en/blog/exponent-rules/
0 Response to "What is the "rule" or shortcut we use when raising an exponent to another exponent?"
Enregistrer un commentaire